Finding the Slope Of A Line From A Table
- Justin Vocke
- Apr 20, 2020
- 2 min read
Updated: Apr 26
Now that we’ve seen how to find the slope of a line from a graph, we can look at how to find the slope of a line from a table (it’s very similar!)
Remember that for now, our equation for finding the slope of a line is given by:
(the triangle symbol is the Greek letter “delta” which means “change” or “change in”)
When we talk about vertical change, we’re talking about the change in y. Horizontal change means the change in x. With that in mind, let’s look at a table of given values for a line:
As a professional math tutor for over 10 years, I created a complete Algebra 1 EOC Exam Review to help students master these skills. It includes 30 practice questions with video solutions! Learn more here!
I’m going to pick the first two coordinates, (0,3) and (1,5) to use and find the vertical and horizontal change between them:
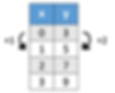
Notice how y increased by 2, and x increased by 1. If we use our slope formula, we get:
We find that the slope of the line is 2. Try two other coordinates and plug them into the slope formula. Do you also get a slope of 2?
Let’s try another example:
Find the slope of the line shown in the following table:
I’m going to find the slope from the first point (2,5) to the second point (4,9):
We see that y increases by 6 when x increases by 2. Let’s plug these into our slope formula:
Let’s try two other points to see if we get the same slope. I’m going to go from the point (4, 11) to (10, 29):
Notice how y increased by 18 and x increased by 6, so let’s plug these into our slope formula:
Notice that despite the fact we used two completely different coordinate points, we got the same slope! Remember that slope is proportional. That means a slope of 18 over 6 is the same as saying a slope of 3 over 1 (just simplifying fractions ;)
This is important to remember moving forward, so try another example before moving on, maybe from (10,29) to (4,11) …(Verify that our slope is 3)
That’s the main idea behind how to find the slope of a line from a table, so our next lesson will be about how to find the slope between two points, and you’ll see how it ties into the lessons we've done so far in finding slope from graphs and tables.
📘 Prepping for your Algebra 1 Final?
Get my full review with 30 key questions + 1.5 hours of video walkthroughs 👉 Check it out here